Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.
这道题给了我们一堆二维点,然后让我们求最大的共线点的个数,根据初中数学我们知道,两点确定一条直线,而且可以写成y = ax + b的形式,所有共线的点都满足这个公式。所以这些给定点两两之间都可以算一个斜率,每个斜率代表一条直线,对每一条直线,带入所有的点看是否共线并计算个数,这是整体的思路。但是还有两点特殊情况需要考虑,二是当两个点重合时,无法确定一条直线,但这也是共线的情况,需要特殊处理。二是斜率不存在的情况,由于两个点(x1, y1)和(x2, y2)的斜率k表示为(y2 - y1) / (x2 - x1),那么当x1 = x2时斜率不存在,这种共线情况需要特殊处理。我们需要用到哈希表来记录斜率和共线点个数之间的映射,其中第一种重合点的情况我们假定其斜率为INT_MIN,第二种情况我们假定其斜率为INT_MAX,这样都可以用map映射了。我们还需要顶一个变量duplicate来记录重合点的个数,最后只需和哈希表中的数字相加即为共线点的总数,这种方法现在已经无法通过OJ了,贴出来权当纪念。代码如下:
C++ 解法一:
// Failed on case: [[0,0],[94911151,94911150],[94911152,94911151]]class Solution {public: int maxPoints(vector & points) { int res = 0; for (int i = 0; i < points.size(); ++i) { unordered_map m; int duplicate = 1; for (int j = i + 1; j < points.size(); ++j) { if (points[i].x == points[j].x && points[i].y == points[j].y) { ++duplicate; } else if (points[i].x == points[j].x) { ++m[INT_MAX]; } else { float slope = (float)(points[j].y - points[i].y) / (points[j].x - points[i].x); ++m[slope]; } } res = max(res, duplicate); for (auto it = m.begin(); it != m.end(); ++it) { res = max(res, it->second + duplicate); } } return res; }};
Java 解法一:
// Failed on case: [[0,0],[94911151,94911150],[94911152,94911151]]public class Solution { public int maxPoints(Point[] points) { int res = 0; for (int i = 0; i < points.length; ++i) { int duplicate = 1, vertical = 0; Map m = new HashMap<>(); for (int j = i + 1; j < points.length; ++j) { if (points[i].x == points[j].x && points[i].y == points[j].y) { ++duplicate; } else if (points[i].x == points[j].x) { m.put(Double.MAX_VALUE, m.getOrDefault(Double.MAX_VALUE, 0) + 1); } else if (points[i].y == points[j].y) { m.put(0.0, m.getOrDefault(0.0, 0) + 1); } else { double slope = (double)(points[j].y - points[i].y) / (points[j].x - points[i].x); m.put(slope, m.getOrDefault(slope, 0) + 1); } } res = Math.max(res, duplicate); for (Map.Entry e : m.entrySet()) { res = Math.max(res, e.getValue() + duplicate); } } return res; }}
由于通过斜率来判断共线需要用到除法,而用double表示的双精度小数在有的系统里不一定准确,为了更加精确无误的计算共线,我们应当避免除法,从而避免无线不循环小数的出现,那么怎么办呢,我们把除数和被除数都保存下来,不做除法,但是我们要让这两数分别除以它们的最大公约数,这样例如8和4,4和2,2和1,这三组商相同的数就都会存到一个映射里面,同样也能实现我们的目标,而求GCD的函数如果用递归来写那么一行就搞定了,叼不叼,这个方法能很好的避免除法的出现,算是牺牲了空间来保证精度吧,参见代码如下:
C++ 解法二:
class Solution {public: int maxPoints(vector & points) { int res = 0; for (int i = 0; i < points.size(); ++i) { map , int> m; int duplicate = 1; for (int j = i + 1; j < points.size(); ++j) { if (points[i].x == points[j].x && points[i].y == points[j].y) { ++duplicate; continue; } int dx = points[j].x - points[i].x; int dy = points[j].y - points[i].y; int d = gcd(dx, dy); ++m[{dx / d, dy / d}]; } res = max(res, duplicate); for (auto it = m.begin(); it != m.end(); ++it) { res = max(res, it->second + duplicate); } } return res; } int gcd(int a, int b) { return (b == 0) ? a : gcd(b, a % b); }};
Java 解法二:
public class Solution { public int maxPoints(Point[] points) { int res = 0; for (int i = 0; i < points.length; ++i) { Map
令我惊奇的是,这道题的OJ居然容忍brute force的方法通过,那么我感觉下面这种O(n3)的解法之所以能通过OJ,可能还有一个原因就是用了比较高效的判断三点共线的方法。一般来说判断三点共线有三种方法,斜率法,周长法,面积法(请参见)。而其中通过判断叉积为零的面积法是坠好的。比如说有三个点A(x1, y1)、B(x2, y2)、C(x3, y3),那么判断三点共线就是判断下面这个等式是否成立:
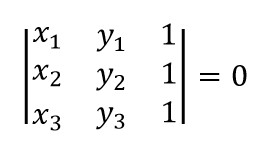
行列式的求法不用多说吧,不会的话回去翻线性代数,当初少打点刀塔不就好啦~
C++ 解法三:
class Solution {public: int maxPoints(vector & points) { int res = 0; for (int i = 0; i < points.size(); ++i) { int duplicate = 1; for (int j = i + 1; j < points.size(); ++j) { int cnt = 0; long long x1 = points[i].x, y1 = points[i].y; long long x2 = points[j].x, y2 = points[j].y; if (x1 == x2 && y1 == y2) {++duplicate; continue;} for (int k = 0; k < points.size(); ++k) { int x3 = points[k].x, y3 = points[k].y; if (x1 * y2 + x2 * y3 + x3 * y1 - x3 * y2 - x2 * y1 - x1 * y3 == 0) { ++cnt; } } res = max(res, cnt); } res = max(res, duplicate); } return res; }};
Java 解法三:
public class Solution { public int maxPoints(Point[] points) { int res = 0, n = points.length; for (int i = 0; i < n; ++i) { int duplicate = 1; for (int j = i + 1; j < n; ++j) { int cnt = 0; long x1 = points[i].x, y1 = points[i].y; long x2 = points[j].x, y2 = points[j].y; if (x1 == x2 && y1 == y2) {++duplicate;continue;} for (int k = 0; k < n; ++k) { int x3 = points[k].x, y3 = points[k].y; if (x1*y2 + x2*y3 + x3*y1 - x3*y2 - x2*y1 - x1 * y3 == 0) { ++cnt; } } res = Math.max(res, cnt); } res = Math.max(res, duplicate); } return res; }}
参考资料: